关于信号与系统中\( \delta \)函数的胡言乱语

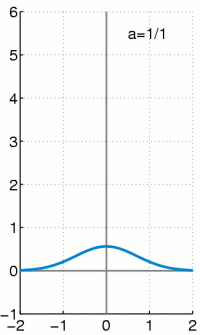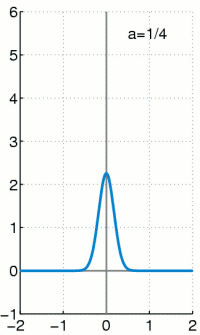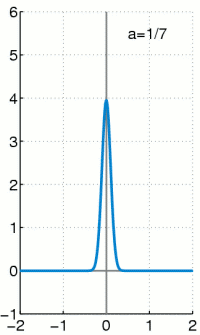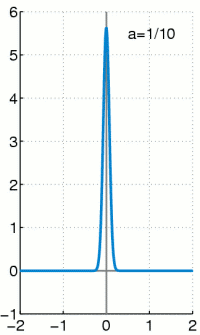
在数学分析中，狄拉克 delta函数（或\( \delta \)分布），也称为单位脉冲，是实数上的广义函数，其值除零外的任何地方都为零，并且其在整个实轴上的积分等于 1。由于没有具有此性质的函数，因此严格地对 delta “函数”建模涉及使用极限，或者像数学中常见的测度理论和分布理论一样。¹

如无特殊声明，本文中提及的\( \delta \)都指的是狄拉克\(\delta\)。

出于工科的应用背景，\(\delta\)函数在常见的信号与系统课程中都有着大量的使用，但是对其定义却鲜有提及，只包含的它的少量性质。常被提及性质的性质有：除零外的任何地方都为零，并且其在整个实轴上的积分等于1。出于这两条性质和信号与系统书上的有些不明所以的推导，我们可以作一些胡言乱语：

\[ \delta(t) =\delta(t) \cdot \frac{t}{t} =\frac{\delta(t)\cdot t}{t} = \frac{0}{t}=0 \]

\[ 0= \frac{d(0)}{dt} =\frac{d(\delta(t) \cdot t)}{dt} = \delta(t) \cdot \frac{dt}{dt}+t \cdot \frac{d(\delta(t))}{dt} = \delta(t) \cdot 1+0 \cdot \frac{d(\delta(t))}{dt}= \delta(t) \]

所以正着反着都证明了一遍，我们可以确信\(\delta(t)=0\)（大雾，只是想说明不讲这个会引起多大的误区

1. 维基百科 Dirac delta function ↩