关于”波光粼粼“的猜测性解释

太阳和灯等光源照在有波纹的水面上，会形成形状复杂的像。本文旨在尝试建立合适的模型来解释这些像的形状。

观察图片可知，在光源视角高度不大且点光源的情况下，像具有非常高的各向异性。而如果仅仅是平面镜成像，像的形状会和光源相同，根本不会有如此明显的各向异性。这引起了笔者很大的好奇，希望解释这种各向异性。

水波

挖坑待填

建模

将水波视为一个随机场，其倾斜角度不超过一个固定的最大值\( \theta_{max} \)​。在任意点的周围，所有小于或等于\( \theta_{max} \)的倾斜角度和方向都是可能的。如果某个点周围的倾斜可以把光线反射到观察者眼中，那么我们就认为这个点是亮的。问题转化为求水面上亮的部分的形状。

在10米以上的长度数量级中处理物体的相互位置关系。因此光的衍射，人眼和路灯泡的尺度可以忽略不计，抽象为点。做出以上简化之后建模。

分析

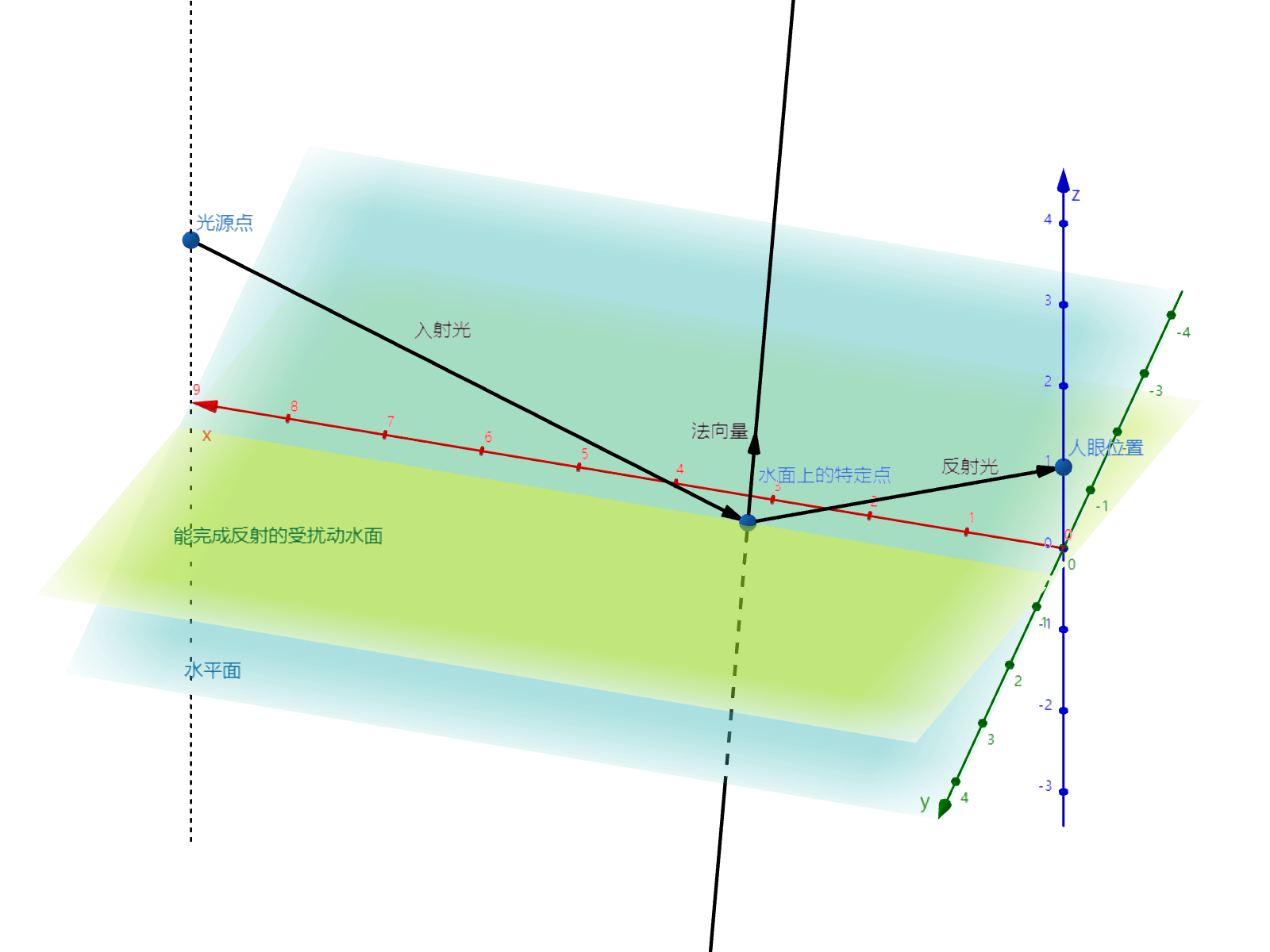如上图建立空间直角坐标系：即以水面为\( xOy \)平面，人眼\( \rightarrow \)光源连线在\( xOy \)方向上投影为x轴正向，竖直向上为z轴正向，人眼在水平面上的投影为坐标原点建立右手空间直角坐标系。

为说明方便，记人眼为\( E \)点，光源为\( S \)点。对于水面上的任意一个点\( P \)，它在人眼中是亮的的充要条件为：入射光\( \vec{SP}\)和反射光\( \vec{PE}\)对应的反射面法向量\( \vec{n}\)和\( z\)轴方向向量\( \hat{z}\)夹角不超过\( \theta_{max}\)。形式化地说，即：

\[\frac{\frac{\vec{PE}}{|\vec{PE}|} + \frac{\vec{PS}}{|\vec{PS}|}}{\left|\frac{\vec{PE}}{|\vec{PE}|} + \frac{\vec{PS}}{|\vec{PS}|}\right|} \cdot \hat{z} \geq \cos\left(\theta\_{max}\right)\]

时，水面时亮的，其余部分水面是暗的。

计算

记人眼高度为\( h_1\)，光源高度为\( h_2\)，两者投影间距为\( d\)。为了更好地将计算出的像和拍摄的照片匹配，对先平面作球极投影，然后将水面完全没有波纹时的光源像旋转至球坐标的一极处，以便更好地比较。Mathmaitca代码实现如下：

f[x_, y_, h1_, h2_, d_] := 
 Normalize[Normalize[{-x, -y, h1}] + Normalize[{d - x, -y, h2}]] . {0,
    0, 1};
fSphere[theta_, phi_, h1_, h2_, d_] := 
 Module[{bx, bz, bn, trans, vori, vtran}, bx = d;
  bz = -h1 - h2;
  bn = Sqrt[bx^2 + bz^2];
  trans = { {bz/bn, 0, bx/bn}, {0, 1, 0}, {-bx/bn, 0, bz/bn} };
  vori = { {Sin[theta] Cos[phi]}, {Sin[theta] Sin[phi]}, {Cos[
      theta]} };
  vtran = trans . vori;
  f[-vtran[[1, 1]]*h1/vtran[[3, 1]], -vtran[[2, 1]]*h1/vtran[[3, 1]], 
   h1, h2, d]];
ParametricPlot3D[{ (* 不等号左边的部分，橙黄色 *)
    theta*Cos[phi],
    theta*Sin[phi],
    fSphere[theta, phi, 1, 10^4, 
    10^4*Cot[(8 + 09/60 + 37.3/3600)/180*Pi]]
   }, { (* 不等号右边的部分，蓝色 *)
    theta*Cos[phi],
    theta*Sin[phi],
    Cos[Pi/180*1.8]
   }}, {theta, 0, Pi/180*4}, {phi, -Pi, Pi},
  Axes -> True, AxesLabel -> {"x/rad", "y/rad", "z"}, 
 PlotPoints -> 100, ViewPoint -> Above, 
 ViewProjection -> "Orthographic"]

结果以及分析解释

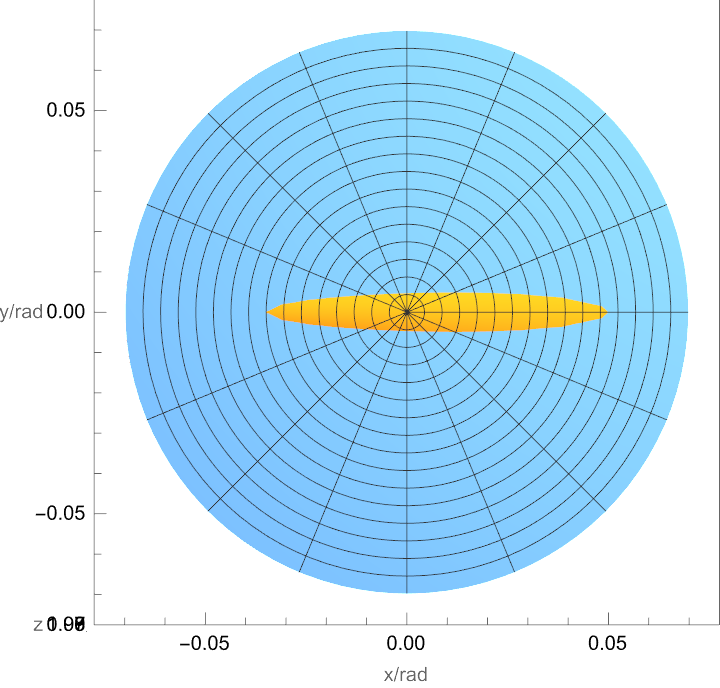
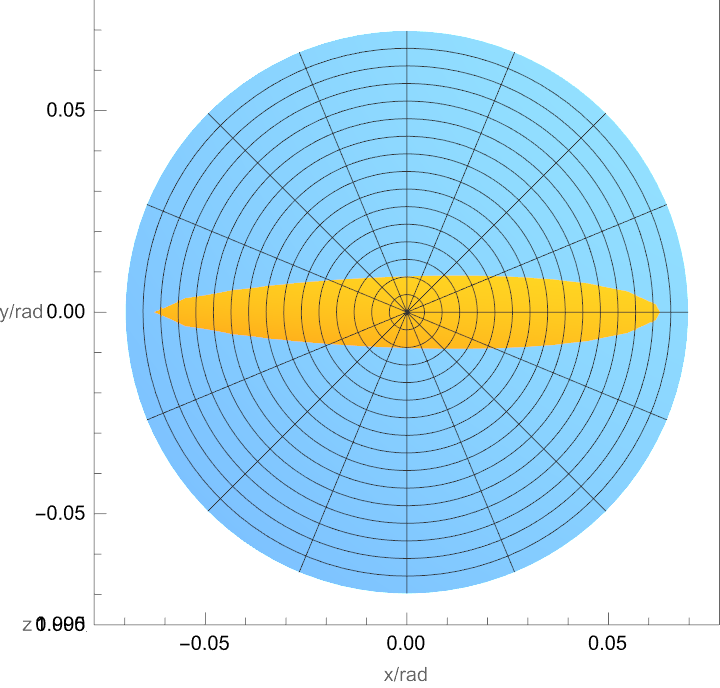
运行代码以得到上图。图的\( x\)轴正方向对应视野中的下方向。路灯的倒影模拟取人眼高度\(1.7\)(m)，路灯高度\(4\)(m)，由地图测量得投影间距约\(53\)(m)。太阳的倒影模拟中照片拍摄时太阳高度角为\(8^\circ 09’ 37.3’’\)。由于日地距离远大于拍摄楼房的高度，人眼高度取\(1\)单位，另外两项分别取\(1e+4\)单位和\(1e+4*cot(8^\circ 09’ 37.3’’)\)单位。

由维基百科，在开阔洋面上，最小等级的浪对应的最大倾角\(\theta_{max}\)约\(3.6^\circ\)。但拍摄用的都是相对小的半封闭水体，线度~100m。这里取其一半（\(1.8^\circ\)）作为估算值。

可以看到，虽然是相对粗略的估计，但是基本还原了的倒影的高度各向异性和大致的形状。

没有合理处理的问题

• 水面不同位置波纹幅度不同
• 没有具体研究水波的行为
• 没有研究和验证光源较高时的情形
• 建模时假设水波方向是各向同性的随机，但实际中未必
• 将太阳（~\(30’\)）和路灯简单处理为点光源，虽然像形状变化随物的位置变化不大，但需要具体计算和卷积
• 图 太阳及其在水中的倒影 中倒影明显不垂直于水平线，文中未能给出合理解释